soal dan pembahasan KONDUKSI KALOR

pepindahan kalor konduksi

No. 1: Soal UNBK dan UNKP 2017 tentang konduksi kalor paket 1

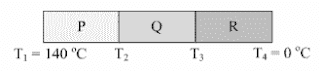
1.      Tiga plat konduktor dengan jenis berbeda - beda disambung seperti gambar di bawah!

Jika perbandingan koefisien konduksi termal logam P , Q , dan R adalah 2 : 1 : 2 .

Besa suhu sambungan T2 dan T3 adalah....

A.      14 ^oC

B.      20 ^oC

C.      35 ^oC

D.     60 ^oC

E.      80 ^oC

Jawaban: C

Pembahasan:

k_P = 2k_Q

2k_Q = k_R

sehingga pebandingannya

2 : 1 : 2

Cara 1

Dengan rumus konduksi / pebandingan:

K1. ΔT1 = K2. ΔT2 = K3. ΔT3

2 . (140 – T2 ) = 1 . (T2 – T3) = 2 . (T3 – 0)

2 . (140 – T2 ) = 1 . (T2 – T3)

280 – 2T₂ = T₂ – T₃

280 = 3T₂ – T₃ ....... pers i

1 . (T₂ – T₃) = 2 . (T₃ – 0)

T₂ = 3T₃....... pers ii

Substitusi:

280 = 3T₂ – T₃ ....... pers i

280 = 3. 3T₃– T₃

280 = 8 T₃

T₃ = 35

T₂ = 3T₃....... pers ii

T₂ = 3.35 = 105 ^oC

Cara 2: Rumus cepat

K bebanding tebalik dengan T

½ : 1 : ½

Atau

1 : 2 : 1

ΔT = T1 – T4 = 140 – 0 = 140

ΔT2 = (1/4).140 = 35

T2 = 140 – 35 = 105

ΔT3 = (1/4).140 = 35

T3 = 35 - 0 = 35

Soal No. 2 : Soal UNBK dan UNKP 2017 tentang konduksi kalor tipe 2

2.      Tiga plat konduktor dengan jenis berbeda - beda disambung seperti gambar di bawah!

Jika perbandingan koefisien konduksi termal logam P , Q , dan R adalah k_P = 2k_Q = k_R.

Besa suhu sambungan T2 dan T3 adalah....

A.      14 ^oC

B.      20 ^oC

C.      35 ^oC

D.     60 ^oC

E.      80 ^oC

Jawaban: C

Pembahasan:

k_P = 2k_Q

2k_Q = k_R

Pebandingan k

2 : 1 : 2

Bisa di kerjakan dengan cara pertama sepeti no 1 di atas. Atau dengan cara 2

Cara 2:

K bebanding tebalik dengan T

½ : 1 : ½

Atau

1 : 2 : 1

ΔT = T1 – T4 = 140 – 0 = 140

ΔT2 = (1/4).140 = 35

T2 = 140 – 35 = 105

ΔT3 = (1/4).140 = 35

T3 = 35 - 0 = 35

3.      Dua buah jenis logam A dan B berukuran sama disambung satu sama lain. Konduktivitas logam A sama dengan tiga kali konduktivitas logam B. Jika suhu di ujung logam B 120^oCdan suhu pada sambungan 90^oC maka suhu pada ujung logam A sebesar adalah … .

A.      60 ^oC

B.      70 ^oC

C.      80 ^oC

D.     90 ^oC

E.      95 ^oC

Jawaban: C

Pembahasan:

K1. ΔT1 = K2. ΔT2

3 . (90 – T) = 1.(120 – 90)

270 – 3T = 30

3T = 240

T = 80 ^oC

4.      Sebuahjendela memiliki ukuran 4 × 2,5 m dengan ketebalan 10 mm. Suhu di dalam ruangan 24 °C dan di luar ruangan 26 °C. Tentukan laju perpindahan kalor dari luar ke dalam ruangan jika konduktivitas termal kaca 0,8 J/s m °C!

Jawaban:

Pembahasan:

rumus laju konduksi kalor

	K . A . ΔT
H =	_________
	L

	0,8 . 4 × 2,5 . (26 – 24)
H =	__________________
	10 . 10-3

H =

1600 J/s

5.      Duabatang logam sejenis penampangnya berbanding 2 : 1 dan panjangnya berbanding 4 : 3. Bila beda suhu ujung-ujung kedua batang sama, maka tentukan perbandingan laju perpindahan kalor pada kedua logam tersebut!

Pembahasan:

 rumus laju konduksi kalor

	K . A . ΔT
H =	_________
	L

K . A . ΔT		K . A . ΔT
_________	=	_________
L		L

4 . 2 .

=

1 . 3

8

:

3

6.      Duabatang logam berukuran sama masing-masing mempunyai koefisien 2k dan k dihubungkan menjadi satu. Kedua logam memiliki ujung bebas yang masing-masing bersuhu 210 °C dan 30 °C. Tentukan besar suhu pada sambungan kedua logam tersebut!

 jawaban:

pembahasan:

dengan rumus cepat / rumus rata - rata

	T1 . k1 + T2 . k2
T =	____________
	k1 + k2

	210 . 2 + 30 . 1
T =	____________
	2+1

T =

150 oC

7. gagang panci tebuat dai kau atau plastik, hal tesebut betujuan....

A. agar laju kalor kecil

B. aga lajur kalo besar

C. plastik adalah konduktor yang baik

D. plastik dan kyau tidak beracun sehingga aman

E. kayu tidak mudah tebaka

8. perhatikan pernyataan beikut!

1. tidak membutuhkan medium dalam perambatan kalor

2. membutuhkan medium dalam perambatan kalor.

3. partikel ikut berpindah membawa kalor.

4. partikel tidak ikut berpindah membawa kalor.

pada proses konduksi kalor konsep yang benar adalah...

A. 1, 2 dan 3

B. 1 dan 3

C. 2 dan 4

D. 4 saja

E. semua benar

jawaban: C

9. saat siang hari yang terik ditreas rumah meskipun tidak terkena matahari secara langsung tapi masih terasa panas, hal tersebut temasuk perpindahan kalor secara...

A. konduksi

B. konveksi

C. radiasi

D. isolasi

E. frustasi

jawaban: B (konveksi)

10. angin darat dan angin laut adalah perpindahan kalor secara....

A. konduksi

B. konveksi

C. radiasi

D. isolasi

E. frustasi

jawaban: B (konveksi)

soal dan pembahasan gerak parabola part 2

Soal No. 11 tentang gerak parabola perpaduan GLB pada sumbu x dan gerak jatuh bebas pada sumbu-y

11. sebuah pesawat tempur pada ketinggian 45 meter ingin menjatuhkan bom dengan sasaran diam yang berada di tanah sejauh 300 m didepan pesawat, agar tepat mengenai sasaran berapakah kecepatan pesawat seharusnya....
a. 20 m/s          d. 200 m/s
b. 50 m/s          e. 250 m/s
c. 100 m/s


jawab: C
pembahasan:

rumus gerak jatuh bebas
mencari waktu bom mendarat di tanah
h = ½ . g . t²
45 = ½ . 10 . t²
t² = 9
t = 3

rumus GLB
s = v . t
300 = v . 3
v = 100 m/s

Soal No. 12
12. sebuah pesawat tempur pada ketinggian 80 m ingin menjatuhkan bom dengan sasaran tank yang berada di tanah pada jarak mendatar sejauh 200 m didepan pesawat, agar tepat mengenai sasaran berapakah kecepatan pesawat seharusnya jika tank bergerak dengan laju 72 km/jam....
a. 30 m/s          d. 240 m/s
b. 60 m/s          e. 250 m/s
c. 120 m/s

kunci jawaban: E
pembahasan:

h = ½ . g . t²
80 = ½ . 10 . t²
t² = 16
t = 4

rumus GLB
mencari jarak yang ditempuh tank selama 4 detik
s = v . t
s = 20 . 4 = 800 m

jarak total:
S = 200 + 800 = 1000 m

s = v.t
1000 = v.4
v = 250 m/s

soal no. 13
sebuah bola tenis menggelinding dari atas meja dengan laju 5 m/s arah mendatar, bola terjatuh dan tepat mengenai lantai setelah menempuh jarak mendatar sejauh 4 meter dari ujung meja. ketinggian meja tersebut sebesar.....
a. 20 cm    d. 1,5 m
b. 50 cm    e. 2 m
c. 1 m

kunci jawaban: A
pembahasan / penyelesaian:


s = v . t
4 = 5 . t
t = 0,2 detik

h = ½ . g . t²
h = ½ . 10 . 0,2²
h = 5 . 0,04
h = 0,2 meter = 20 cm

soal no.14

sebuah bola tenis menggelinding dengan laju 4 m/s arah mendatar dari atas meja setinggi 1,8 m, kecepatan bola setelah bergerak 0,2 detik sebesar.....
a. 4 m/s             d. 3 √3 m/s
b. 2 √5  m/s       e. 2 m
c. √5 m

kunci jawaban: A
pembahasan / penyelesaian:

pada sumbu x:
vx = 4 m/s

pada sumbu y:
vy = g.t
vy = 10 . 0,2 = 2

besar kecepatan di dapat dari resultan vektor kedua kecepatan:
v² = vx² + vy²
v² = 4² + 2²
v² = 16 + 4
v² = 20
v = 2 √5 m/s

soal no.15

sebuah bola tenis menggelinding dengan laju 4 m/s arah mendatar dari atas meja setinggi 1 m, kecepatan bola saat berada pada ketinggian 0,8 m dari tanah adalah...
a. 4 m/s             d. 3 √2 m/s
b. 4 √2  m/s       e. 5 m/s
c. 4 √5 m/s

kunci jawaban: A
pembahasan / penyelesaian:

pada sumbu x:
vx = 4 m/s

pada sumbu y:
h = 1 - 0,8 = 0,2 m dari posisi awal

Vy² = 2gh
Vy² = 2.10.0,2 = 4

besar kecepatan di dapat dari resultan vektor kedua kecepatan:
V² = Vx² + Vy²
V² = 4² + 4²
V² = 32
V = √32 m/s
V = 4√2 m/s

soal sebelumnya:
<<< pembahasan gerak parabola (perpaduan GLB dan GVA)

soal dan pembahasan RLC part 2/2

soal N0.6
6. Sebuah hambatan R jika diberi tegangan bolak balik 220 V yang bekerja pada frekuensi 50 Hz mampu mengalirkan arus 2 A. Tentukan:

a. Besar kapasitansi kapasitor yang harus dipasang seri dengan hambtan itu agar dapat mengalirkan arus 1 A
b. Sudut fase antara V dan I

Pembahasan / penyelesaian :

V = I .R
220 = 2 . R
R = 110 Ω

a. Kapasitas kapasitor (XC)

jika I = 1 A
V = I . Z
220 = 1 . Z
Z = 220 ohm

Z² = R² + Xc ²
220² = 110² + Xc²
Xc ² = 220² - 110²
Xc² = (2.110)² - 110²
Xc² = 4 . 110² - 110²
Xc² = 3 . 110²
Xc = 110 √3

b. Sudut fase

Tan φ = [ Xc/R ]

Tan φ = √3

φ = 60°

Soal No. 7 rangkaian LC
7. Sebuah induktor murni dipasang dengan kapasitor. Selanjutnya ujung-ujung rangkaian ini dihubungkan dengan sumber tegangan bolak balik 100 V dengan frekuensi sudut 50 rad/s. Jika arus yang mengalir pada rangkaian 2 A dan tegangan pada ujung-ujung induktor 150 V, tentukan kapasitansi kapasitor!

Jawab : C
Pembahasan / penyelesaian:
V = 100 V
I = 2A
ω = 50 rad / s

VL = 150 V
C .... ?

Pada rangkaian induktor L dan kapasitor C tanpa resistor R
Vtot = VL - Vc
100 = 150 - Vc
Vc = 50 V

Vc = I . Xc
50 = 2 . Xc
Xc = 25 ohm

Xc = 1/(ω.C)
25= 1/(50 . C)
C = 1/1250
C = 8 . 10^-4 Farad

Soal No. 8 frekuensi tesonansi pada rangkaian RLC
8. Jika kapasitor 25 pF dipasang seri dengan induktor L = [1/4π²) H, frekuensi resonansi rangkaian ini adalah...

Jawab:
Pembahasan / penyelesaian :



soal no.99. Sebuah induktor murni dengan induktansi L = (5/π²) mH dipasang seri dengan kapasitor. Ujung-ujung rangkaian ini dihubungkan dengan sumber AC supaya beresonansi pada frekuensi 1 MHz. Tentukan kapasitansi kapasitornya!

Pembahasan:
Saat resonansi Xc = XL

C = 1/(4π².f.L)
C = 1 / ( 4.π².10⁶ . (5/π²) . 10^-3 )
C = 1/(20.10^-3)
C = 500 Farad

soal no. 10
10. Dalam suatu rangkaian, arus bolak balik sebesar I mengalir melalui resistor 6 ohm, induktor yang mempunyai XL = 2 ohm dan kapasitor yang mempunyai XC = 10 ohm.



ab adalah titik antara R
bc adalah titik antara XL
cd adalah titik antara Xc

Jika diketahui Vbc = 10 V, tentukan nilai Vab, Vcd dan Vad!

Penyelesaian / pembahasan:

Impedansi

Z² = R² + (XL - Xc)²
Z² = 6² + 8²
Z = √100
Z = 10 ohm

Perbandingan tegangan dan hambatan R , XL dan Xc

 VR : R = VL : XL = Vc : Xc = Vtot : Z

VR : 6 = 10 : 2 = Vc : 10 = Vtot : 10

VR : 6 = 10 : 2
VR = 6.5 = 30 Volt

10 : 2 = Vc : 10
Vc = 5.10 = 50 Volt

10 : 2 = Vtot : 10
Vtot = 5.10 = 50 Volt

baca selengkapmya >>>
 > soal dan pembahasan RLC part 1/2
 > soal dan pembahasan RLC part 2/2

pembahasan soal RLC arus dan tegangan AC part 1/2

Soal dan pembahasan rangkaian seri RLC (rasistor, induktor dan kapasitor) pada arus dan tegangan bolak balik ( AC )
Soal 1 : Soal esai / uraian RLC
Resistor (R) , kapasitor (C) dan induktor (L) dirangkai seri dan dihubungkan dengan sumber tegangan bolak balik (AC) dengan voltase maksimum sebesar 26√2 V dan kecepatan sudut 200 rad/s seperti gambar!


Jika R = 12 ohm, C = 500 μF dan L = 75 mH. Hitung:
a. Reaktansi induktif
b. Reaktansi kapasitif
c. Jenis atau sifat rangkaian
d. Impedansi
e. Arus maksimum
f. arus efektif

Pembahasan soal / Penyelesaian:
a. Reaktansi induktif (XL) 
XL = ω . L = 200 . 0,075 = 15 ohm

b. Reaktansi kapasitif (Xc)
Xc = 1/ω.C
Xc = 1/200.500.10 -⁶
Xc = 10 ohm

c. Jenis rangkaian

Rangkaian diatas bersifat induktif karena XL > Xc, sehingga arus (I) ketinggalannya sebesar 90° terhadap tegangan (V)

d. Impedansi (Z) pada rangkaian RLC

Z² = R² + (XL - Xc)²
Z² = 12² + (15 - 10)²
Z² = 144 + 25
Z² = 169
Z = √169
Z = 13 Ohm

e. Arus maksimum

I = V / Z
I = 26√2 / 13
I = 2√2 Ampere

f. arus efektif
Ief = Imax / √2
Ief = 2√2 / √2
Ief = 2 Ampere

soal No. 2 :
perhatikan rangkaian RLC berikut!

jika R = 40 ohm, XL = 60 ohm dan Xc = 90 ohm, dan dihubungkan dengan tegangan AC dengan nilai maksimum sebesar 25√2 Volt. berapakah nilai daya desipasi pada rangkaian tersebut?

pembahasan / penyelesaian

Z² = R² + (Xc - XL)²
Z² = 40² + 30²
Z² = 2500
Z = 50 ohm

Imax = Vmax/Z
Imax = 25√2/50
Imax = 0,5√2 A

Ief = Imax/√2
Ief = 0,5√2/√2 = 0,5 A

Daya desipasi
P = Ief ² . Z
P = 0,5² . 50
P = 0,25 . 50
P = 12,5 watt

Soal No.3 : soal uraian / esai RC
3.Sebuah hambatan 750 Ω dan sebuah kapasitor 2,5 μF disusun seri, kemudian ujung-ujungnya dihubungkan dengan sumber AC 25 V yang memiliki frekuensi 200/π Hz. Tentukan :

a. Impedansi rangkaian
b. Tegangan antara ujung-ujung hambatan

Pembahasan / Penyelesaian:
Rumus ω
ω =2.π.f
ω =2.π.[200/π.]
ω =400 rad/s

Rumus Reaktansi kapasitif (Xc)
Xc = 1/ω.C
Xc = 1/(400.2,5.10 -⁶)
Xc = 1000 ohm

Rumus Impedansi (Z) pada rangkaian R-C
Z² = R² + Xc²

Z² = 750² + 1000²

Z² = 1562500

Z = √1562500

Z = 1250 ohm

Tegangan pada resistor (VR)
VR : R = Vtot : Z

VR : 750 = 25 : 1250

VR : 750 = 1 : 50

VR = 750 / 50

VR = 15 Volt

Soal RLC no 4
4. Arus bolak balik dengan frekuensi sudut 1 x 10⁴rad/s mengalir melalui rangkaian seri hambatan 10 Ω dan kapasitor 0,1 μF. Jika beda potensial pada ujung-ujung hambatan adalah 20 V, tentukan beda potensial pada ujung-ujung kapasitor!

Penyelesaian / pembahasan :
Diketahui :
ω = 1 x 10⁴ rad/s 
R =  10 Ω
C = 0,1 μF
V = 20 V

Rumus Reaktansi kapasitif (Xc)
Xc = 1/(ω.C)
Xc = 1/(10⁴ . 10^-5)
Xc = 10 ohm

Rumus Impedansi (Z) pada rangkaian R-C
Z² = R² + Xc²

Z² = 10² + 10²

Z² = 200

Z = 10√2 ohm

Tegangan pada kapasitor (Vc)
Vc : Xc = Vtot : Z

Vc : 10 = 20 : 10√2

Vc = 2 : √2

Vc = 0,5 √2 Volt

Soal RLC no.5 
5.Sebuah hambatan 400 ohm dan sebuah kapasitor disusun seri, kemudian ujung-ujungnya dihubungkan dengan sumber AC 200 V yang memiliki frekuensi 50 Hz. Jika tegangan pada ujung-ujung hambatan adalah 160 V, tentukan :
a.      Tegangan pada ujung-ujung kapasitor
b.      Reaktansi kapasitor

Pembahasan / penyelesaian:

a. Tegangan pada kapasitor

V² = VR ²+ Vc²
200² = 160²+Vc²
Vc² = 40000-25600
Vc² = 14400
Vc = √1400
Vc = 120 Volt

b. Reaktansi kapasitor

Vc : Xc = VR : R
120 : Xc = 160 :400
Xc = 300 ohm

baca selengkapmya >>>
 > soal dan pembahasan RLC part 1/2
 > soal dan pembahasan RLC part 2/2